一:一阶系统响应定义
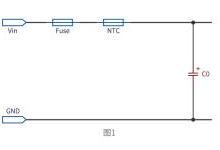
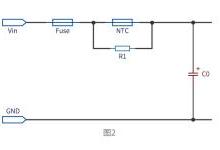
通常来讲,一阶系统分为电压驱动一阶系统(a)以及电流驱动一阶系统(b),如下图所示:

这两个一阶系统在线路上是完全等效的。它们的阶跃响应如下:

电压或者电流的上升时间在这里定义为从10%开始,上升到90%结束所需要的时间。对于一阶系统,可以推导出上升时间为:


带宽定义为AC输入信号激励下输出响应幅值降到直流信号幅值的70.7%(或-3dB)所对应的频率。
一阶系统的传递函数表达式如下:

由此可以推导出一阶系统的带宽为:

由以上数学表达式,我们很容易得出一阶系统的上升时间与带宽的关系为:

由此可知,一阶系统的上升时间与带宽成反比,这也就是为什么我们经常说带宽变宽,系统响应速度会变快的理论解释。
二:一阶系统在低频和高频下的近似响应
从一阶系统的传递函数,我们知道一阶系统的幅值,相角以及群延时的表达式如下:

其中群延时是表征系统中频率信号所经历的延时时间。
一阶系统只有一个极点,接下来我们看看此一阶系统在低频和高频下的行为是怎么样的,低频或者高频都是相对极点频率所言。对于高频,我们假定wτ?1,此时一阶系统的幅值、相角以及群延时近似为:

因此,对于高频一阶系统,传递函数的幅值近似以20dB/十倍频的速度衰减,相移近似为-90度,群延时随着频率的平方减少,频率高的信号比频率低的信号群延时要少。
对于低频信号,即wτ?1,我们可以近似得到如下传函:

因此,对于低频一阶系统,传递函数的幅值近似为单位1,负的相移与频率近似成线性关系。群延时只与时间常数有关,也就是说,极点会贡献有限的相移。比如频率比极点频率低10倍频的频率点,极点会贡献约-5.7度的相移。如果负的相移过大,就会引起系统振荡。