本文将简单介绍信号处理技术最基本的知识,拉普拉斯变换,传递函数以及零极点。
任何线性时不变系统的传递函数以及零极点都可以用电子元器件在拉普拉斯变换域(或者s域)内的阻抗形式进行表示。从电路到拉普拉斯变换域(或者s域)内的转换形式如下表所示:

另外s域还代表着微分方程,替代关系如下:

任何线性时不变系统的传递函数都可以用含有s的多项式方式进行表述,如下式所示:

当H(s)的分母为0时,所得到的s值被称为极点;当H(s)的分子为0时,所得到的s值被称为零点。因此,上述传函中,有n个零点以及m个极点。
上述传递函数的零点以及极点的值既可以是实数根也可以是虚数根。如果是实数根,当输入是阶跃信号时,输出响应是一个简单的指数响应曲线(e^(-t/τ),没有超调或者振铃产生。如果极点是复数根,根会成对出现,如果阻尼不是足够大,输出响应会产生振铃。
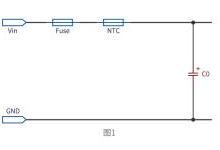
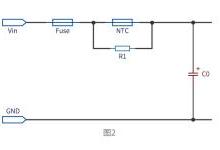
举一个简单的电路系统为例,此电路系统由两个电阻以及一个电容组成。我们很容易根据以上方法把此电路系统(a)转换为s域系统(b)。

由此,我们得到输入输出传递函数:

根据此传递函数,我们很容易得到如下结论:
1. 在非常低的频率(频率接近于0,直流信号),可以等效为s→0,于是得到:

电路意义很清楚,在直流情况下,电容相当于开路,输出就等于输入;
2. 在非常高的频率(频率趋向于∞),可以等效为s→∞,于是得到:

电路意义也很清楚,当频率趋向于无穷大,电容相当于短路,电阻分压比决定输出。
3. 此传递函数的零极点如下:

下一节将简单介绍一阶系统的响应。