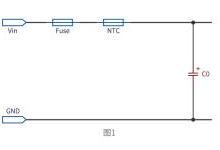
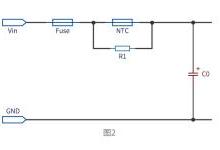
一:LC 谐振电路基础
考虑如下的LC谐振电路:

这是典型的LC谐振电路,存储在电容中的电场能量与存储在电感中的磁场能量以频率wr进行周期性的交换。我们假设电路初始条件为电感电流为0,电容电压为Vc。此时电感电流的差分方程为:

同样,电容电压的差分方程为:

由以上两个方程我们可以得到此LC谐振电路的系统方程为:

解此方程我们可知电容电压与电感电流都是标准的正弦波形,而且频率都是wr。

二:能量分析方法
能量分析方法是分析无阻尼谐振电路最基本也是最有效的方法。能量可以是存储在电容中的电场能量(Capacitor/Electric field storage),存储在电感中的磁场能量(Inductor/Magnetic field storage),运动物体的能量(Kinetic energy),旋转物体的能量(Rotary energy),弹簧系统储能(Spring energy), 势能(Potential energy)以及蓄热体储能(Thermal energy)等。

而且通过能量分析方法,我们很容易解出谐振电路中电容最大电压与电感最大电流之间的比例。我们假设电容初始电压为Vo,因此存储在电容中的电场能量为:

存储在电感中的磁场能量为:

因为无阻尼,通过能量相等,我们得到:

因此:

Zo在谐振电路中被定义为谐振电路的特征阻抗。我们假设谐振电容C=1mF,电感L=1mH。因此可以得出谐振频率为166.7kHz,特征阻抗为1ohm,下图是仿真波形。

当然我们也可以用能量分析方法来分析弹簧系统的振荡频率。存储在弹簧中的弹性势能为:

质点的运动动能为:

通过能量相等,我们可以得出:

下一节将简单介绍零极点、传递函数以及波特图的基础知识。