大家好,在上一篇文章中,我们介绍了FJSP问题以及HA算法的GA部分。这一篇文章主要介绍嵌套在其中的Tabu Search部分。
种群进化+邻域搜索的混合算法(GA+TS)求解作业车间调度问题(JSP)-算法介绍
Tabu部分原论文没有很详细的描述,因此很多内容是小编收集各方资料,查阅其他相关文献总结出的结论,小编自己编写了三个tabu search,在这里分别分享介绍一下。如有专门研究这块的同学,欢迎随时指点交流!
代码会在下一期统一给出,请关注我们!
Tabu1-基于编码
在之前的文章中说过,算法对每一代子代的每一个个体,都需要decode成可行解,然后运用禁忌搜索优化解,再编码回GA编码,进入下一代。可想而知,如果tabu写的不好,算法的耗时肯定会很高。
论文中的tabu其实是以第二种为主体的。基于编码的tabu相对而言比较盲目,当初编写时也是基于试一试的心态。
前文提到,对一串合法的OS序列,无论进行怎样的交换、插入运算,都可以解码成可行解;对MS序列,在同一工件范围内任意交换顺序,也可以保证得到可行解。
因此,小编在代码中简单设计了两种邻域:1. 对相邻的OS编码进行交换操作;2. 对MS编码的每个位置分别采用GA中的变异操作。
swap很简单,再重复一下MS的变异:
随机选择MS中一半的数字,随机换为对应操作可以选择的某个机器。例如图中长度为6的MS String,随机选择三个位置,对O11而言,共有三个机器可选择,则随机选择1,2,3中一个数字替换掉原先的2。
邻域部分代码(开启了一个50%的采样):
for (int i = 0; i < chromosome.gene_OS.length - 1; i += 2)
for (int j = i + 1; j < chromosome.gene_OS.length; j += 2)
if(r.nextDouble() < 0.5)
OSs.add(swap(chromosome.gene_OS, i, j));
for (int i = 0; i < chromosome.gene_MS.length; i++)
if(r.nextDouble() < 0.5){
int[] MS = chromosome.gene_MS.clone();
MSs.add(chromOps.machineSeqMutation(MS));
}
结论:这个邻域设计的比较随意,但经过小编的测试后发现效果不佳,小编在这里建议大家不要使用基于编码的邻域搜索。
Tabu2-基于析取图的k-insertion
析取图
对JSP和FJSP来说,除了用甘特图表示解意外,还有一个很重要的表示解的结构:析取图。
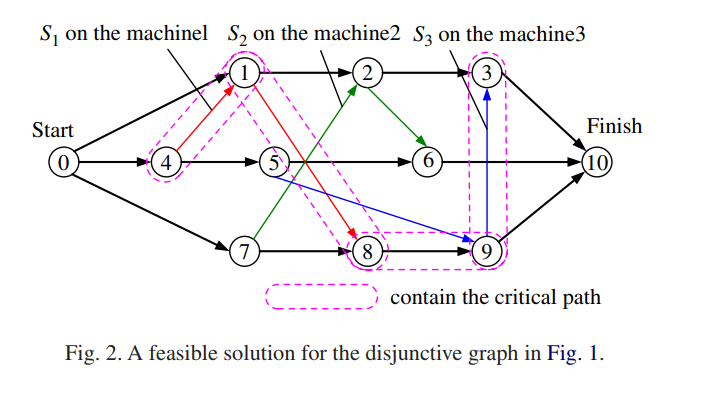
析取图是一张有向图。图中的点表示工序,边代表工序加工的顺序。










